オタクof数理の共同ブログ

京大情報学科数理工学コースの学生4人による共同ブログです

正則言語

よねすけ 数学 計算理論

こんにちは, よねすけです.

正則言語

正則言語とは正則表現で表される言語のことです. 同値な表現方法として以下があります.

すなわち上の4つの表現方法はいずれも能力として等価であるということです.

正則言語の閉包性

正則言語には閉包性という性質があります. 具体的には正則言語L_1,L_2について,

  • \overline{L_1}は正則言語
  • L_1\cup L_2は正則言語
  • L_1\cap L_2は正則言語

などです. それぞれ証明しましょう.

証明

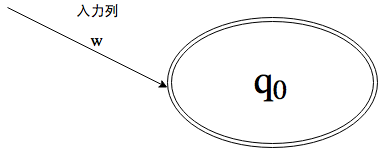
  • L_1は正則言語なのである{\rm DFA} Aで認識される言語です. A=(Q,\sum,\delta,q_0,F)として, 次のオートマトンBを考えます. B=(Q,\sum,\delta,q_0,Q-F)とすると, 受理状態と非受理状態が綺麗に入れ替わることが分かるのでL(B)=\overline{L_1}となり, \overline{L_1}も{\rm DFA}で受理できることが分かりました. よって\overline{L_1}も正則言語です.
  • L_1,L_2は正則言語なのである正則表現R_1,R_2を用いて, L_1=L(R_1),L_2=L(R_2)と書くことが出来ます. このとき正則表現の書き方からL(R_1+R_2)はL_1\cup L_2と一致することが分かります. よって正則言語の和集合もまた正則表現になることが分かります.
  • L_1\cap L_2=\overline{\overline{L_1}\cup\overline{L_2}}がド・モルガンの公式から分かるので上に証明したことから正則言語の積集合もまた正則言語であることが分かります.

正則言語の閉包性の証明には正則表現の4つの表現方法をうまく活用することで簡単に示すことが出来ます.

正則言語の性質

正則言語の性質としてPumping Lemmaがあります.

Pumping Lemma

Lを正則言語とします. あるn\in\mathbb{N}で, 長さn以上のすべてのw\in Lに対してw=xyzと分解します. そうするとx,y,zについて

  • y\ne\varepsilon
  • |xy|\le n
  • k\in\mathbb{Z}_{\ge 0}に対して, xy^kz\in L

です.

Pumping Lemmaは正則言語そのものよりも考える言語が正則言語で無いことを示す事によく使われます. 例えばL_{01}=\{0^i1^i|i\ge 1\}が正則言語でないことはPumping Lemmaの逆から示されます.


それでは

チューリングマシンが受理する言語

よねすけ 計算理論 数学

こんにちは, よねすけです.

今回はチューリングマシンの話を書きたいと思います. 以下チューリングマシンをTMと省略します.

帰納的可算集合(Recursively Enumerable)

言語Lが帰納的可算集合であるとは, あるTMMによって

L=L(M)
と書けることを言います. この集合を{\rm RE}と書く事があります.

帰納的集合(Recursive)

言語Lが帰納的集合であるとは, ある必ず止まるTMMによって

L=L(M)
と書けることを言います. この集合を{\rm R}と書くことがあります. この定義から明らかなように
{\rm R}\subset{\rm RE}
が分かります. {\rm R}に含まれる言語は必ず止まるTMによって認識出来るので可解であることも分かります.
このような言語は色々あります. 一番簡単な言語はalphabet\sumからなる列全体を集めた次の言語
L_3=\sum^*
じゃないでしょうか. これを認識するTMはすべての入力に対して初期状態と受理状態を一致させることによって設計できます. 状態遷移図は次のようになります.

f:id:otaku_of_suri:20170127135742p:plain

このときTMは1ステップで必ず止まるのでL_3は帰納的集合であることが分かります.

このような集合の他にそもそもTMで認識出来ない集合もあります. そのような言語の例として空集合問題や対角線言語があります. 空集合問題において考える言語は

L_e=\{M|L(M)=\phi\}
です. 空集合問題は一般に非可解である, すなわち{\rm R}に含まれないことはよく知られていますが, {\rm RE}にすら実は含まれないということはとても驚きでした.
対角線言語において考える言語は
L_d=\{\sigma_i|{\rm TM}\sigma_iは\sigma_iを受理しない\}
です. この言語が対角線論法を用いて示されることでも有名です.

それでは

愛情の数学

cajihara 数学

こんにちは．かじはらです．
クリスマスが近いので愛にまつわる数学の話をしたいと思います．

以前よねすけくんが無理数の無理数乗が有理数になる，という話をしていました．

otaku-of-suri.hatenablog.com

では複素数の複素数乗が実数になることはあるのでしょうか？

まずは複素数の複素数乗を定義しなければなりません．

{ \begin{align*} &z,w \in \mathbb{C}\\ &z^w = e^ {\log{z^w}} = e^{w \log z} \end{align*} }

対数を使って定義するんでしたね．
複素数の対数がどのように定義されていたかもついでにおさらいしておきましょう．

{ \begin{align*} \log z &= \log re^{i \theta}\\ &= \log r + \log e^{i \theta}\\ &= \log r + i \theta + 2 \pi n i \end{align*} }

複素数の対数は一意に値が定まらない多価関数になるんでしたね．

前回も虚数の話をしたので話題が重複してしまって申し訳ありませんが，今回も虚数に登場してもらいましょう．

{ \displaystyle i^i }
これはまさしく複素数の複素数乗の一種です．これを上の定義に則って計算してみましょう．

{ \begin{align*} i^i &= e^{\log{i^i}}\\ &= e^{i \log i}\\ &= e^{i \log e^{\frac{\pi}{2}i}}\\ &= e^{i \log e^{(\frac{\pi}{2}+ 2n \pi)i}}\\ &= e^{-(\frac{\pi}{2}+ 2n \pi)} \end{align*} }

よくわからない式がでてきました．これではどんな値が具体的にはわからないですね．
しかしここで注目すべきはそこではありません．よく見てください．

なんと虚数が消えています！！！！！！！！！

計算結果は実数の実数乗の形をしているので，具体的な値はわからずともこの値が実数であることは確かです．

つまり，

愛(i)の愛情(i乗)は実数になる！！！！！！！



え…？愛にまつわる数学ってこれ…？ここにきてダジャレ…？ダジャレなの…？

という声が聞こえてきそうですね．

（調べたところ「i^i乗」というwikipediaの項目もあるぐらいなのでかなり有名な話っぽいですが，
高１の時にこの事実を知って以来お気に入りの数学小話(?)のひとつなので，どうしても書きたかったのです．）


次回は，

高校数学の試験で「{a_{n+1}=f(a_n)}の数列の極限を求めよ．」という形式の問題が出された時，{\alpha = f(\alpha)}を解いて{\alpha}を極限値として答えを求める方法がなぜダメなのか？

について考察します．（かじはらの気分が年明けあたりまで変わらなければ．）

おしまい．

答え

よねすけ 数学

こんにちは,よねすけです.

前回の記事で,

otaku-of-suri.hatenablog.com

最後に証明を残したところがあるので,それだけ示したいと思います.示すべきことは0{<}q{<}1において

\displaystyle\sum_{n=1}^{\infty}\frac{q^n}{1-q^n}<\infty

です.二通りほど示し方を考えました.
ダランベールの収束判定法を用いる
ダランベールの収束判定法を使えば簡単に示せます.

\displaystyle a_n=\frac{q^n}{1-q^n}

と置くと,n\to\inftyで

\displaystyle\frac{a_{n+1}}{a_n}=\frac{q^{n+1}}{1-q^{n+1}}\cdot\frac{1-q^n}{q^n}=q\cdot\frac{1-q^n}{1-q^{n+1}}\to q<1

となるので示せました.

ちょっとテクる
うまい(?)方法を思いついたので書いてみます.q<1なのでqと1の中点を取ると

\displaystyle q{<}\frac{q+1}{2}{<}1

となります.これを使うと

\displaystyle q^n<\frac{q+1}{2}\iff\frac{1}{1-q^n}<\frac{2}{1-q}

が分かります.これをはじめの式に適用すると

\displaystyle\sum_{n=1}^{\infty}\frac{q^n}{1-q^n}{<}\frac{2}{1-q}\sum_{n=1}^{\infty}q^n=\frac{2q}{(1-q)^2}

となり示されました.

それでは.

おもろい式

よねすけ 数学

こんにちは,よねすけです.
明日はじめて阪大に行くのが楽しみすぎて眠れない.遠足の前の日みたいや.

高木貞治の『解析概論』をぼーっとめくってたら

定本 解析概論

定本 解析概論

オモロい式を見つけました.

\displaystyle\frac{q}{1-q}+\frac{q^3}{1-q^3}+\frac{q^5}{1-q^5}+\cdots=\frac{q}{1-q^2}+\frac{q^2}{1-q^4}+\frac{q^3}{1-q^6}+\cdots

ただし,|q|<1です.普通に証明するのは簡単やった.

\displaystyle\begin{eqnarray} (左辺)&=&\sum_{n=0}^{\infty}\frac{q^{2n+1}}{1-q^{2n+1}}\\ &=&\sum_{n=0}^{\infty}q^{2n+1}\left(\sum_{m=0}^{\infty}\left(q^{2n+1}\right)^m\right)\\ &=&\sum_{n=0}^{\infty}\left(\sum_{m=0}^{\infty}q^{(2n+1)(m+1)}\right)\\ (右辺)&=&\sum_{n=0}^{\infty}\frac{q^{n+1}}{1-q^{2(n+1)}}\\ &=&\sum_{n=0}^{\infty}q^{n+1}\left(\sum_{m=0}^{\infty}\left(q^{2(n+1)}\right)^m\right)\\ &=&\sum_{n=0}^{\infty}\left(\sum_{m=0}^{\infty}q^{(2m+1)(n+1)}\right)\\ &=&\sum_{m=0}^{\infty}\left(\sum_{n=0}^{\infty}q^{(2n+1)(m+1)}\right) \end{eqnarray}

となります.なのであと示すべきことはこの無限和が交換できることです.二重級数は絶対収束すれば足し算の順番を交換しても大丈夫なのでこいつらが絶対収束することを示しましょう.示すべきことは

\displaystyle\sum_{n,m=0}^{N}|q|^{(2n+1)(m+1)}\leq M

なるMがNの値によらずに存在することです.こいつが案外厄介.

\displaystyle\begin{eqnarray} \sum_{n,m=0}^{N}|q|^{(2n+1)(m+1)}&\leq&\sum_{n=0}^{N}\frac{|q|^{2n+1}}{1-|q|^{2n+1}}\\ &\leq&\sum_{n=1}^{\infty}\frac{|q|^n}{1-|q|^n} \end{eqnarray}

こいつが有界である(収束する)ことは各自頑張って証明してみて下さい*1.

(無限和)=(無限和)の形やから,ポアソンの和公式から示せたらエレガントやなあ,とか思った.

それでは.

*1:ここに証明をいくらか書いてみました.良かったら読んで下さい. otaku-of-suri.hatenablog.com

そもそも虚軸ってなんなの

cajihara 数学

こんにちは．かじはらです．

今日はこんな問題を考えてみます．

{ \displaystyle x^2 = -1 }

この式を「一次元の世界の計算」と呼んでおきましょう．

これは考える範囲を複素数としなければ解をもたず．

{ \displaystyle x = \pm i }

となります．簡単ですね．

さて，複素数はどんなものかといわれたら多くの人が次の式を思い起こすと思います．

{ \displaystyle z = x + iy　(z \in \mathbb{C},\, x,y \in \mathbb{R}) }

複素数を座標で表すときに，ちょうどこのxを直交座標のx軸に対応させて実軸と呼び，yをy軸に対応させて虚軸と呼びました．

式で見ると当然のように思えますがそもそもなぜ虚軸をy軸と対応させたのでしょうか．

そこでいったんさっきの問題をわきに置いて次の問題を考えたいと思います．

{ \displaystyle \left( \begin{array}{cc} a & b \\ c & d \end{array} \right)\left( \begin{array}{cc} a & b \\ c & d \end{array} \right) = \left( \begin{array}{cc} -1 & 0 \\ 0 & -1 \end{array} \right)\\ が成り立つような実数a,b,c,dを求めよ． }

実際に計算すればわかることですがこの問題の解は実は無数にあります．ここでは最も簡潔だと思われる

{ \displaystyle \left( \begin{array}{cc} 0 & -1 \\ 1 & 0 \end{array} \right) }

を採用しましょう. この行列を{ \displaystyle X }と置き，最初の問題を書き直すと

{ \displaystyle X^2 = -I }

となります．これを「二次元の世界の計算」と呼びましょう．最初に考えた「一次元の世界の計算」と形がとても似ていますね．

「一次元の世界」で掛け算を考えたとき，その単位元は「1」です。その世界で「ある一次の行列を２乗すると-1になる数」を考えようとすると実数の範囲では答えが見つからず，複素数という概念を導入しなければならなくなりました．

「二次元の世界」で掛け算を考えたとき，その単位元は「{ \displaystyle I }」です．「ある二次の行列を２乗すると{ \displaystyle -I }になる数」を考えるとちゃんと実数の範囲で答えが見つかります．

ここまでくると一次元だった(実数の)直線を複素数に拡張しよう，つまり虚数単位を導入しようとするとき，二次元である平面を考える発想はとても自然なことに思えてきませんか？

ではなぜ虚軸は「x軸と直交をなすy軸」なのでしょうか．単に平面を考えるだけなら別に直交していなくてもいいはずですよね．（まあ直交してるものを考えるのが一番わかりやすいじゃん，と言われてしまうとその通りなのですが．）

行列{ \displaystyle X }をこんな風に書き換えてみましょう．

{ \displaystyle X = \left( \begin{array}{cc} 0 & -1 \\ 1 & 0 \end{array} \right) =\left( \begin{array}{cc} \cos 90^\circ & -\sin 90^\circ \\ \sin 90^\circ & \cos90^\circ \end{array} \right) }

回転行列がでてきました．つまり「二次元の世界」で{ \displaystyle X^2 = -I}の解となる行列（のひとつ）は直交座標を90度回転させるようなものだということになります．

つまり実軸を(正の符号を採用すれば反時計回り，負の符号なら時計回りに)90度回転させたものが虚軸に対応する，ということが，こう書くととても腑に落ちますね．わーい．



なんだかまわりくどく書いてしまいました．

そもそもどうしてこんなことを書いたかと言うと，高校数学の新課程に関して，素人ながら少し思うことがあったからです．

高校数学の新課程では行列がなくなり，複素平面が復活しました．

でも，今までの議論を思い出すと，この新課程には違和感を覚えます．

今日本屋で高校数学の参考書の複素平面のページを見たら，最初に

{ \displaystyle z = x + iy　(z \in \mathbb{C},\, x,y \in \mathbb{R})\\ i = \sqrt{-1} }

こういう式がいきなり書いてあるものが多くて，それ以降は共役がどうの，絶対値がどうの，といったことが書いてあって．

高校の頃，どうやって複素平面について学んだのかはよく覚えてませんが，もし今の自分が誰かに複素平面について説明しろ，と言われたら最初の行列の概念を使うと思うんです．だから行列を消して，複素数を復活させる，ということが，自分にとってはむずがゆい．


…偉そうに高校数学に文句を言ってしまいました．すみません．

最後まで読んでくれた方，ありがとうございます．

おしまい．

半球の体積の求め方

cajihara 数学

こんにちは。かじはらです。なんと2015年8月以来の投稿になります。

前回の投稿で株はじめる宣言をしたかじはらでした。
otaku-of-suri.hatenablog.com


しかしすっかり飽きてしまったというか、毎日朝に株価のチェックをするのが面倒で、今はほとんど売ってしまいました。

持っていた株を売るときにあまりにも買値よりも下がってしまっていたものだけ今手元に置いているのですが、この前久々に確認したらだいぶ値段が戻ってきてたことと、少ないながらももらえる配当金のことを考えると、まあ持ったままでいいかな、と思って放置しています。



さて本題。今日は以下の問題について考えます。

「半径rの半球の体積Vを求めなさい」

答えが { \displaystyle V = \frac{2}{3} \pi r^3 } であることはあまりによく知られた結果ですね。

（球の体積の公式を習ったとき、それを微分すると球の表面積になることに気付いた瞬間はなんとも言えない感動がありましたが、今思えば、微分や積分の意味を理解していなかった証拠かもしれません。）

この問いにガリレオ・ガリレイが全く別の解法を提示していたことを最近知りました。

日常現象からの解析学

日常現象からの解析学

↑この本の中で紹介されてました。好き。

新科学対話〈上,下〉 (1949年) (岩波文庫)

新科学対話〈上,下〉 (1949年) (岩波文庫)

↑ちなみに元ネタはこの本の中に。



まず半径r高さrの円柱にこの半球をすっぽりと埋もれさせたものの断面を考えます。

f:id:otaku_of_suri:20161203170422p:plain

さらに次のような補助線をひいてみます。
f:id:otaku_of_suri:20161203170641p:plain
添え字がごちゃごちゃしていて見にくいですね。ついでに言うと最初の図との大きさのバランスも悪いですね。ごめんなさい。

さて、ここで半球ではなく、この補助線によって現れた円錐と、円柱から半球をくりぬいた図形に対応する臼のような形の図形に着目してみましょう。

このGHの面でスパッと切ったときの臼に対応する図形の断面積Sは
{ \displaystyle S = \pi (GH^2 - HI^2) }
と表せます。ここでピタゴラスの定理より、
{ \displaystyle HI^2 = FI^2 - FH^2 }
が成り立ちます。

さらに、GHは半球の半径に対応することからGH=FI、この円錐の断面が直角二等辺三角形であることからFH=JHが成り立ちます。

よってこれらを代入すると
{ \displaystyle S = \pi (FI^2 - (FI^2 - JH^2))= \pi JH^2 }
となり、臼の断面積が円錐の断面積と一致することがわかります。これは円柱の底面に水平になるように切断することを考えれば、円柱内の任意の断面について成り立ちます。

これより円錐の体積は
{ \displaystyle \frac{1}{3}×(円柱の体積) }
ですので、半球の体積は
{ \displaystyle V = \frac{2}{3}×(円柱の体積)=\frac{2}{3} \pi r^3 }
であることがわかりました。


こんな補助線の引き方、そう簡単に思いつくものじゃないと思います。（少なくとも自分には無理。）


余談ですが、ガリレオが亡くなった年はニュートンが生まれた年でもあります。なんだか運命的ですね。

おしまい。