オタクof数理の共同ブログ

京大情報学科数理工学コースの学生4人による共同ブログです

円筒座標系におけるrotの表示

よねすけ 数学

夏休みいかがお過ごしでしょうか。よねすけです。
今日は成績発表でしたね。僕は一科目だけ落としてたので異議申し立てするか迷っています。

今回は円筒座標系におけるrotがどう表されるかについて書きたいです。（だいぶ昔の）ゼミの教科書で当たり前のように出てきてびっくりしました。

まず、ユークリッド座標系でのベクトルは円筒座標系ではどのように表されるのでしょうか。
計算の方法としては直交座標\{x,y,z\}から円筒座標\{\rho,\phi,z\}への変数変換を考えます。

\begin{eqnarray} x&=&\rho\cos\phi\\ y&=&\rho\sin\phi\\ z&=&z\\ \end{eqnarray}

それぞれの座標系での基底ベクトルを定めます。直交座標については、
{\boldsymbol e}_x= \left( \begin{array}{c} 1\\ 0\\ 0 \end{array} \right),{\boldsymbol e}_y= \left( \begin{array}{c} 0\\ 1\\ 0 \end{array} \right),{\boldsymbol e}_z= \left( \begin{array}{c} 0\\ 0\\ 1 \end{array} \right)

円筒座標については、
{\boldsymbol e}_{\rho}= \left( \begin{array}{c} \rho\cos\phi\\ \rho\sin\phi\\ 0 \end{array} \right),{\boldsymbol e}_{\phi}= \left( \begin{array}{c} {-}\rho\sin\phi\\ \rho\cos\phi\\ 0 \end{array} \right),{\boldsymbol e}_z= \left( \begin{array}{c} 0\\ 0\\ 1 \end{array} \right)

ただしこれらベクトルは直交座標ののるものとします。
このとき適当なベクトル{\boldsymbol A}このような式を考えることができます。
{\boldsymbol A}=A_{x}{\boldsymbol e}_{x}+A_{y}{\boldsymbol e}_{y}+A_{z}{\boldsymbol e}_{z}=A_{\rho}{\boldsymbol e}_{\rho}+A_{\phi}{\boldsymbol e}_{\phi}+A_{z}{\boldsymbol e}_{z}

{\boldsymbol e}_{x},{\boldsymbol e}_{y},{\boldsymbol e}_{z}は互いに直交することに注意すれば、
A_{x}=A_{\rho}{\boldsymbol e}_{\rho}\cdot{\boldsymbol e}_{x}+A_{\phi}{\boldsymbol e}_{\phi}\cdot{\boldsymbol e}_{x}

であり、
\begin{eqnarray} {\boldsymbol e}_{\rho}\cdot{\boldsymbol e}_{x}&=&\cos \phi\\ {\boldsymbol e}_{\phi}\cdot{\boldsymbol e}_{x}&=&-\sin \phi \end{eqnarray}

を用いれば、
A_{x}=A_{\rho}\cos \phi-A_{\phi}\sin \phiとなる事が分かります。A_{y}=A_{\rho}\sin \phi+A_{\phi}\cos \phiも同様に示せます。
よって、
{\boldsymbol A}= \left( \begin{array}{c} A_{\rho}\cos \phi-A_{\phi}\sin \phi\\ A_{\rho}\sin \phi+A_{\phi}\cos \phi\\ A_{z}\\ \end{array} \right)

がわかりました。

次に
{\boldsymbol \nabla}={\boldsymbol e}_{x}\partial_{x}+{\boldsymbol e}_{y}\partial_{y}+{\boldsymbol e}_{z}\partial_{z}を円筒座標系で表示する事を考えます。
これは極座標の場合と同じで、

\begin{eqnarray} \partial_{\rho}&=&\cos \phi \partial_{x} +\sin \phi \partial_{y}\\ \partial_{\phi}&=&-r\sin \phi \partial_{x}+r\cos \phi \partial_{y} \end{eqnarray}

より、
\begin{eqnarray} \partial_{x}&=&\cos \phi \partial_{\rho}-\frac{1}{r}\sin \phi \partial_{\phi}\\ \partial_{y}&=&\sin \phi\partial_{\rho}+\frac{1}{r}\cos\phi\partial_{\phi} \end{eqnarray}

が言えるので、
{\boldsymbol \nabla}= \left( \begin{array}{c} \cos \phi \partial_{\rho}-\frac{1}{r}\sin \phi \partial_{\phi}\\ \sin \phi\partial_{\rho}+\frac{1}{r}\cos\phi\partial_{\phi}\\ \partial_{z}\\ \end{array} \right)

がわかります。
以上より、
\begin{eqnarray} {\boldsymbol \nabla} \times {\boldsymbol A}&=&\left( \begin{array}{c} \partial_x\\ \partial_y\\ \partial_{z}\\ \end{array} \right)\times\left( \begin{array}{c} A_x\\ A_y\\ A_z\\ \end{array} \right)\\ &=&\left( \begin{array}{c} \cos \phi \partial_{\rho}-\frac{1}{r}\sin \phi \partial_{\phi}\\ \sin \phi\partial_{\rho}+\frac{1}{r}\cos\phi\partial_{\phi}\\ \partial_{z}\\ \end{array} \right)\times\left( \begin{array}{c} A_{\rho}\cos \phi-A_{\phi}\sin \phi\\ A_{\rho}\sin \phi+A_{\phi}\cos \phi\\ A_{z}\\ \end{array} \right)\\ \end{eqnarray}

これを各成分について計算して整理すると、(ここは計算が煩雑なので省略しました)
\begin{eqnarray} {\boldsymbol \nabla}\times{\boldsymbol A}=\left(\frac{1}{\rho}\partial_{\phi}A_z-\partial_zA_{\phi}\right){\boldsymbol e}_{\rho}+(\partial_zA_{\rho}-\partial_{\rho}A_z){\boldsymbol e}_{\phi}+\frac{1}{r}(\partial_{\rho}(\rho A_{\rho})-\partial_{\phi}A_{\rho}){\boldsymbol e}_{z} \end{eqnarray}

がわかります。z方向については直交座標と何も変わらないので{\boldsymbol \nabla},{\boldsymbol A}のz方向については何も計算しなくても良かったですね。最後の計算がほんまにめんどくさいです。
それでは。

前期の振り返りするで。

よねすけ

こんばんは、よねすけです。
3回前期が無事に(?)終わったのでいつもの様に振り返りを。今期は受けた授業がどれも面白かったです。

月曜2限：工業数学A2
数値計算に関する授業でした。数値計算アルゴリズムをいっぱい聞けてその歴史についても少し学べたので面白いと思いました。ほんとは全部自分で実装とかしないとダメなんだろうな、とか思いながらも結局ヤコビ法 - Wikipediaしか実装しませんでした。まあ実際使うときになったら実装しましょうね。
試験は授業の内容から証明問題が出たり、実際に近似計算させたり、という感じの問題でした。僕はパデ近似(Padé approximation)を覚えていませんでした、はい。ちゃんと勉強しましょう。

月曜3,4限：数値計算演習
はい、鬼門の実験です。正直、授業中に先生やTAにきちんと質問していればそんなにしんどくは無かったと思います。僕は授業中に怠けてしまって課題をためてしまったので提出日前日にモンスターエナジーを導入するハメになりました。課題はまじめにこなしましょうね。個人的にはパーコレーションのシミュレーッションが面白かったです。(課題の一つはこのURLに上がっています。http://www-fcs.acs.i.kyoto-u.ac.jp/~harada/education.html)

火曜2限：確率離散事象論
火曜日はこのコマしかなかったので、この授業終わったらきらめきJAPANに行こうかな、にぼに行こうかな、みたいなことを考えながら授業を受けていました。授業は待ち行列モデルに関するものでした。確率を正確に扱えるならば特に難しくありません。むしろ僕はこの授業で確率の計算をきちんと扱えるようになった気がします。
試験は授業から満遍なくでました。レジュメをしっかり理解して、基礎事項をきちんと覚えていれば問題無いでしょう。

水曜1限：工業数学A3
Fourier解析に関する授業です。Fourier解析をただ計算できるってだけじゃなくて解析的に厳密に扱えるようにしておきましょうね、っていう授業でした。僕はこういう授業も大切だな、と思います。
試験は演習問題と似たような問題が出ました。演習問題が解ければ問題無いでしょう。

水曜2限：確率と統計
確率と統計、名前の通りの授業です。途中から何をやっているか分からなくなった、と言っている人が結構いました。分からない時はその場できちんと復習しましょうね、といった所かな。
試験は授業から満遍なく出ました。計算力があって授業を理解していれば問題はなさそう。

水曜3限：人工知能
これもタイトル通りの授業。ほんまにこう言うのがあるよっていう感じでした。内容は一つ一つはとてもおもしろいとは思いましたが、正直苦手なタイプの授業でした。
試験は論述ばっかりでした。きちんとレジュメを読みましょう。僕は山を外して一題まるまるほぼ白紙でした。

水曜4限：力学系の数学
力学系の授業です。最高です。おもしろい。内容は面白いんやけど、それ以上に先生の雑談(?)が面白かったです。
試験は演習問題が解ければ特に問題なく解ける問題になっています。

木曜2限：物理統計学
僕が個人的に一番好きな授業でした。ブラウン運動、ランジュバン方程式などなど盛り沢山なイメージでした。
試験はレポート問題から1題、授業から1題でした。レポート問題をきちんと復習すれば難なくこなせるでしょう。

木曜4限：数理解析
超関数の基礎と超関数を用いた有名偏微分方程式の基本解の導出が主でした。今までの微積分のいろいろな定義を拡張していく感じ(?)が個人的に面白かったです。拡張する前に1回生の微積分をしっかり分かっとけや？って言われないようにしましょうね。
試験はなくてレポートのみです。分かっていれば、難しくはないです。分かっていれば、ですが。
金曜2限：振動・波動論
2回生の時に取り損ねたので取りました笑。恥ずかしいのでスルーしましょう。

金曜3限：非線形動力学
統計力学の基本的事項に始まり、数理生態のモデルの解析、集団引き込み転移の解析、スケールフリーネットワークの理論など幅広く扱った授業でした。スライドでシミュレーションの様子も見れて面白いなあと思いました。レポートが3回出ました。1回も出しませんでした笑。
試験はレポートが理解できていれば特に問題ありません。

こんな感じですね。夏休みはしっかり学び、働き、遊び、3回後期に備えたいと思います。
それでは。

試験のヤマのはりかた！

zalgo 雑記

こんにちは。ざるご（@zalgo3）です。

ぼくは今定期試験の真っ最中です。小中高校生の人はもう試験は終わって夏休みなのかな？
というわけで今日はヤマはりについての話題です。

よく試験でヤマなんかはるな！全部ちゃんと勉強しろ！って言う人がいます。
まあ、それも一理あるんですけど、ヤマをはることってのはそんなに悪いことなんでしょうか？
先生が試験に出しそうなところ＝重要なところ
です。そこをしっかりやるっていうのはその教科の理解に大きく貢献するでしょうね。
でも、ヤマはったら違うとこが出ておおコケした！赤点取っちゃった！なんて人もいるんじゃないでしょうか。
そういう人って、この図みたいなヤマのはりかたをしてるような気がします。
f:id:otaku_of_suri:20160727164518p:plain
こうすることはあまりオススメしません。勉強したとこが出なかった時のリスクが大きすぎますね笑
それに、しっかり勉強した範囲が出たとしても、意外と問題が簡単で、ちゃんと勉強したのが報われなかった・・ってなりかねません。

僕のおすすめはこうです！
f:id:otaku_of_suri:20160727164523p:plain
でなさそうなとこも、ちょっとはやりましょう！万が一出たとしてもその問題が最低限0点にはならずにすみます。
でも、結構メリハリはつけちゃって大丈夫だと思います！一番出そうなとこはスラスラ書けるくらいにしときたいですが、そこまででもないところにそんなにまじめに付き合ってあげなくても良さそうです。

ざるごでした。それではまた〜

弾性体の振動の縦波と横波

よねすけ 物理

よねすけです。振動波動論の試験で弾性体の振動に関する問題が出て勉強してなくて全く分かりませんでした。つらい。。。

弾性体中の座標ベクトル\textbf{r}の点の、時間tにおける変位を\textbf{u}(\textbf{r},t)とすると、弾性体の振動の方程式は

\displaystyle\rho\partial^2_{t}\textbf{u}=\frac{E}{2(1+\mu)}\left[\nabla^2\textbf{u}+\frac{1}{1-2\mu}\nabla(\nabla\cdot\textbf{u})\right]

で与えられます。ここで\rhoは弾性体の密度、Eはヤング率、\muはポアソン比です。(いずれも定数、\displaystyle 0<\mu<\frac{1}{2})

定ベクトル\textbf{u}_0を用いて\displaystyle\textbf{u}\left(\textbf{r},t)=\textbf{u}_0{\rm exp}(i(\textbf{k}\cdot\textbf{r}-\omega_k t)\right)と書けたとします。これを先の振動の式に代入して整理すると

\displaystyle\rho\omega_k^2\textbf{u}_0=\frac{E}{2(1+\mu)}\left[k^2\textbf{u}_0+\frac{1}{1-2\mu}\textbf{k}(\textbf{k}\cdot\textbf{u}_0)\right]

が得られます。
縦波の場合、すなわち考える波の進行方向と媒質の振動方向が平行な場合、
\textbf{k}\parallel\textbf{u}_0

が言えます。\textbf{k}(\textbf{k}\cdot\textbf{u}_0)=k^2\textbf{u}_0を代入すれば
\displaystyle\rho\omega_k^2\textbf{u}_0=\frac{E}{2(1+\mu)}\left[k^2\textbf{u}_0+\frac{k^2}{1-2\mu}\textbf{u}_0\right]

です。縦波の速さをv_lとおくと\omega_k=v_l kなので
\displaystyle v_l=\sqrt{\frac{(1-\mu)E}{(1+mu)(1-2\mu)\rho}}

が分かりました。

横波の場合、すなわち考える波の進行方向と媒質の振動方向が垂直な場合、

\textbf{k}\cdot\textbf{u}_0=0

が言えます。
\displaystyle\rho\omega_k^2\textbf{u}_0=\frac{E}{2(1+\mu)}k^2\textbf{u}_0

横波の速さをv_tとおくと\omega_k=v_t kなので
\displaystyle v_l=\sqrt{\frac{E}{2(1+mu)\rho}}

が分かりました。

縦波、横波の速さを比較してみましょう。

\displaystyle\begin{eqnarray} \left(\frac{v_l}{v_t}\right)^2&=&\frac{(1-\mu)E}{(1+\mu)(1-2\mu)\rho}\frac{2(1+\mu)\rho}{E}\\ &=&1+\frac{1}{1-2\mu}\\ &>&2 \end{eqnarray}

これより、v_l>\sqrt{2}v_tが分かります。
地震のP波(=v_l)の速さはおよそ5\sim 7km/s、地震のQ波(=v_t)の速さはおよそ3\sim 4km/sと言われているそうなのでだいたい一致していますね。

それでは。

無理数の無理数の無理数の・・・

よねすけ 数学

こんにちは。世の大学生は試験前で忙しい頃ですね。僕ももれなく忙しいです。試験勉強頑張りましょうね。

少し前にtsujimotterさんのこの記事が話題になりました。
tsujimotter.hatenablog.com
この記事では\displaystyle\sqrt{2}^{\sqrt{2}}を用いて無理数の無理数乗の中で有理数になるものが存在することの証明を行っていました。結果から言うと\displaystyle\sqrt{2}^{\sqrt{2}}は超越数になります。(このことは
ゲルフォント＝シュナイダーの定理 - Wikipediaを用いるとすぐに分かります。)
では、次の値を考えてみましょう。

\LARGE{\displaystyle\sqrt{2}^{\sqrt{2}^{\sqrt{2}^{\sqrt{2}^{\sqrt{2}^{\sqrt{2}^{\sqrt{2}^{\sqrt{2}^{\sqrt{2}^{\sqrt{2}^{\sqrt{2}^{\sqrt{2}^{\sqrt{2}^{\cdots}}}}}}}}}}}}}}

なんじゃこれ、そもそも収束するのか？？って思わせる式ですね。
でもこれ、きちんと収束してくれるんですよ。しかも有理数に。不思議ですよね。\displaystyle\sqrt{2}^{\sqrt{2}}は超越数になるのに、その操作を無限回行うと有理数になる。無限というものの神秘を感じます。
以下に証明を示します。証明は理系の高校生ならわかるとてもシンプルなものになっています。
\displaystyle\sqrt{2}^{\sqrt{2}^{\sqrt{2}^{\sqrt{2}^{\sqrt{2}^{\sqrt{2}^{\sqrt{2}^{\sqrt{2}^{\sqrt{2}^{\sqrt{2}^{\sqrt{2}^{\sqrt{2}^{\sqrt{2}^{\cdots}}}}}}}}}}}}}=2

(証明)
与えられた式を次のように数列を用いて漸化式で書き換えます。
\displaystyle a_n=\sqrt{2}^{a_{n-1}},a_0=\sqrt{2},s.t.\lim_{n\to\infty}a_n=2

証明すべきことはa_nが2に収束することです。
まずa_n<2を数学的帰納法により示します。n=0の時は明らかです。あるnでa_n<2だとすると
a_{n+1}=\sqrt{2}^{a_n}<\sqrt{2}^2=2

となりn+1の場合も示されました。以上よりa_n<2です。
次にf(x)=\sqrt{2}^xという関数を考えます。
\displaystyle f'(x)=(\log{\sqrt{2}})\sqrt{2}^x

となります。ここで平均値の定理を考えると区間(a_n,2)で
\displaystyle\frac{f(2)-f(a_n)}{2-a_n}=f'(c_n)

なるc_nが存在します。c_n<2が分かっているのでf'(c_n) <\log 2です。これより
\begin{eqnarray*} &&f(2)-f(a_n)=f'(c_n)(2-a_n)\\ &\Rightarrow&2-a_{n+1}<(\log 2)(2-a_n) \end{eqnarray*}

が分かります。あとはこれを順番に用いると
\begin{eqnarray*} 0<2-a_{n}&<&(\log 2)(2-a_{n-1})\\ &<&(\log 2)^2(2-a_{n-1})\\ &&\cdots\\ &<&(\log 2)^n(2-a_0) \end{eqnarray*}

となります。\log 2<1よりn\to\inftyの極限で
2-a_n\to 0\Leftrightarrow a_n\to 2

となりました。以上より\displaystyle\lim_{n\to\infty}a_n=2が示されました。
高校生でも理解できる簡単な証明ですね。(これは多分同志社大学の数学の入試問題やった。)
一般にaが自然対数の底eよりも小さな1以上の実数なら
\begin{eqnarray*} \sqrt[a]{a}^{\sqrt[a]{a}^{\sqrt[a]{a}^{\sqrt[a]{a}^{\sqrt[a]{a}^{\sqrt[a]{a}^{\sqrt[a]{a}^{\sqrt[a]{a}^{\sqrt[a]{a}^{\sqrt[a]{a}^{\sqrt[a]{a}^{\cdots}}}}}}}}}}}=a \end{eqnarray*}

が成立します。極限は奥が深いですね。
それでは。

数学のメモその３

よねすけ 数学 フーリエ変換

今回は、一旦ゼータ関数を置いといてフーリエ解析に関することを書きます。
授業の中でPlancherel(プランシュレル)の定理というものを習いました、

Plancherelの定理
f,g,\hat{g}\in L^1(\mathbb{R})\Rightarrow \langle\hat{f},\hat{g}\rangle=\langle f,g\rangle

f\in L^1(\mathbb{R}):有界連続\Rightarrow\|f\|=\|\hat{f}\|\ (f,\hat{f}\in L^2(\mathbb{R}))

というものなんですが授業ではさらっと流されて証明もプリントで、、、みたいな感じやったんですけどこの定理は結構面白いことを言ってるんじゃないかなあと思いました。

適当な正規直交関数系\displaystyle \{f_i (x)\}_{i=1}^{\infty}を一つ考えてみましょう。正規直交関数系とは

\begin{equation} \langle f_i,f_j\rangle=\delta_{i,j} \end{equation}

を満たすもののことです。勘の良い方はこれで僕が何を言いたいのか分かったかも知れませんね笑。この関数が{}^{\forall}i\in\mathbb{N}に関してf_i(x)\in L^2(\mathbb{R})などなど適当な条件を満たしているとしましょう。f_iのFourier変換を\mathcal{F}f_i=\hat{f}_iと書くことにすると、
\langle \hat{f}_i,\hat{f}_j\rangle=\langle f_i,f_j\rangle=\delta_{i,j}

がプランシュレルの定理から分かります。これが何を意味しているかというと適当な条件を満たす正規直交関数系をひとつ持ってこればそれをFourier変換して得られる系もまた正規直交関数系となるのです！！

教授氏にこのことについて質問してみると、チェビシェフの多項式においてこのことが成り立つそうです。また時間があるときに確かめてみたいです。
それでは。

数学のメモその２

よねすけ 数学 バーゼル問題

前回に続き\displaystyle\zeta(2)=\frac{\pi^2}{6}の証明を書きたいと思います。
〜２重積分を用いる〜
この証明は２重積分

\begin{eqnarray} I=\int_0^1\int_0^1\frac{1}{1-xy}dxdy \end{eqnarray}

の値を２通リに求めることからわかります。１つ目は\displaystyle\frac{1}{1-xy}を等比級数\sum_{n\ge 0}(xy)^nに展開することです。
\begin{eqnarray} I&=&\int_0^1\int_0^1(xy)^ndxdy=\sum_{n\ge 0}\int_0^1\int_0^1x^ny^ndxdy\\ &=&\sum_{n\ge 0}\left(\int_0^1x^ndx\right)\left(\int_0^1y^ndy\right)=\sum_{n\ge 0}\frac{1}{n+1}\frac{1}{n+1}\\ &=&\sum_{n\ge 0}\frac{1}{(n+1)^2}=\sum_{n\ge 1}\frac{1}{n^2}=\zeta(2) \end{eqnarray}

Iの２つ目の計算方法は変数変換です。
\displaystyle u=\frac{y+x}{2},\ v=\frac{y-x}{2}

と変数変換します。するとx=u-v,y=u+vより
\displaystyle\frac{1}{1-xy}=\frac{1}{1-u^2+v^2}

である。またヤコビアンは2である。
f:id:otaku_of_suri:20160703141457p:plain
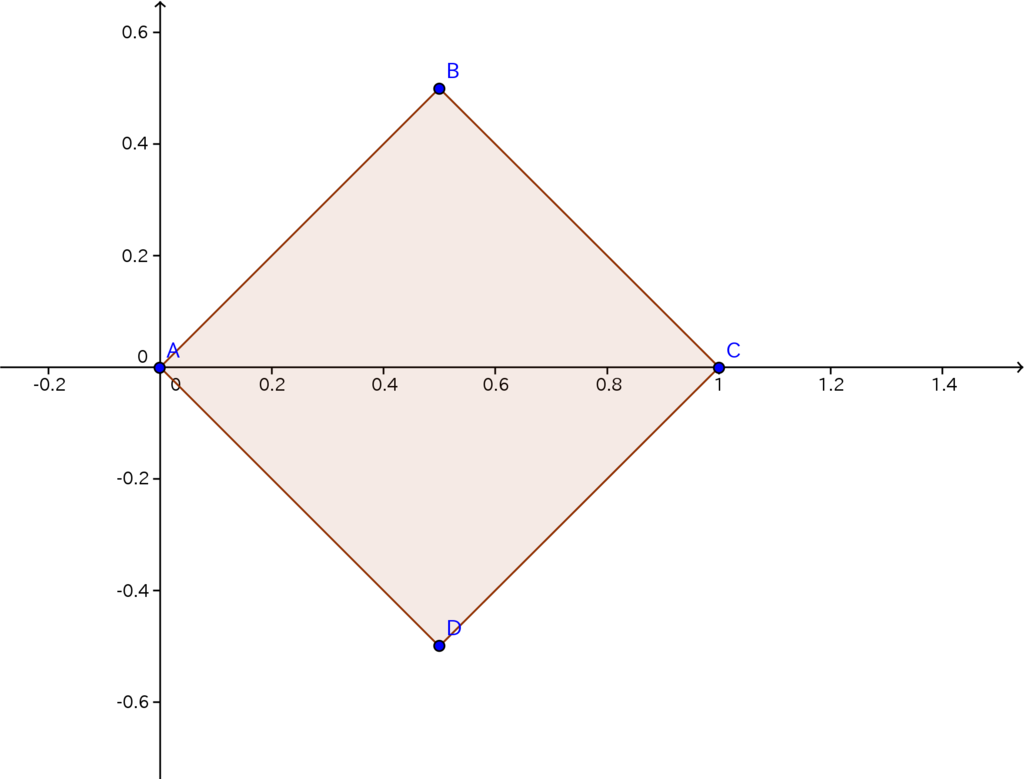
変数変換後の積分領域は上の図の色がけ部であるから\displaystyle u\le \frac{1}{2}と\displaystyle u\ge \frac{1}{2}に分けて積分する。またvに関して対称であることも考慮すると
\begin{eqnarray} I&=&4\int_0^{\frac{1}{2}}\left(\int_0^u\frac{dv}{1-u^2+v^2}\right)du+4\int_{\frac{1}{2}}^1\left(\int_0^{1-u}\frac{dv}{1-u^2+v^2}\right)du\\ &=&4\int_0^{\frac{1}{2}}\frac{1}{\sqrt{1-u^2}}\arctan\left(\frac{u}{\sqrt{1-u^2}}\right)du\\ &&+4\int_{\frac{1}{2}}^1\frac{1}{\sqrt{1-u^2}}\arctan\left(\frac{1-u}{\sqrt{1-u^2}}\right)du \end{eqnarray}

となります。ここで\displaystyle\int\frac{dx}{a^2+x^2}=\frac{1}{a}\arctan{\frac{x}{a}}+Cを用いました。
ここでu=\sin\thetaとおくと、\displaystyle\frac{u}{\sqrt{1-u^2}}=\frac{\sin\theta}{\cos\theta}=\tan\thetaであるから結局、\displaystyle\arctan{\frac{u}{\sqrt{1-u^2}}}=\arcsin uとなります。
またu=\cos\thetaとおくと、\displaystyle\frac{1-u}{\sqrt{1-u^2}}=\frac{1-\cos\theta}{\sin\theta}=\frac{2\sin^2\frac{\theta}{2}}{2\cos\frac{\theta}{2}\sin\frac{\theta}{2}}=\tan\frac{\theta}{2}であるから結局、\displaystyle\arctan{\frac{1-u}{\sqrt{1-u^2}}}=\frac{1}{2}\arccos uとなります。よって、
\displaystyle I=4\int_0^{\frac{1}{2}}\frac{\arcsin u}{\sqrt{1-u^2}}du+2\int_{\frac{1}{2}}^1\frac{\arccos u}{\sqrt{1-u^2}}du

がわかります。ここで第１項の積分についてはu=\sin\theta、第２項の積分についてはu=\cos\thetaと変数変換すると
\begin{eqnarray} I&=&4\int_0^{\frac{\pi}{6}}\frac{\theta}{\cos\theta}\cos\theta d\theta+2\int_{\frac{\pi}{3}}^{0}\frac{\theta}{\sin\theta}(-\sin\theta)d\theta\\ &=&4\int_{0}^{\frac{\pi}{6}}\theta d\theta+2\int_{0}^{\frac{\pi}{3}}\theta d\theta\\ &=&4\left[\frac{\theta^2}{2}\right]^{\frac{\pi}{6}}_{0}+2\left[\frac{\theta^2}{2}\right]^{\frac{\pi}{3}}_{0}\\ &=&4\frac{1}{2}\frac{\pi^2}{36}+2\frac{1}{2}\frac{\pi^2}{9}=\frac{\pi^2}{6} \end{eqnarray}
となります！！！以上より
\displaystyle\zeta(2)=\frac{\pi^2}{6}

が示されました。

あと１つ証明があるのでそれはまた今度ということで。