数学のメモその２ - オタクof数理の共同ブログ

前回に続き $\displaystyle\zeta(2)=\frac{\pi^2}{6}$ の証明を書きたいと思います。
〜２重積分を用いる〜
この証明は２重積分

$\begin{eqnarray} I=\int_0^1\int_0^1\frac{1}{1-xy}dxdy \end{eqnarray}$

の値を２通リに求めることからわかります。１つ目は $\displaystyle\frac{1}{1-xy}$ を等比級数 $\sum_{n\ge 0}(xy)^n$ に展開することです。
$\begin{eqnarray} I&=&\int_0^1\int_0^1(xy)^ndxdy=\sum_{n\ge 0}\int_0^1\int_0^1x^ny^ndxdy\\ &=&\sum_{n\ge 0}\left(\int_0^1x^ndx\right)\left(\int_0^1y^ndy\right)=\sum_{n\ge 0}\frac{1}{n+1}\frac{1}{n+1}\\ &=&\sum_{n\ge 0}\frac{1}{(n+1)^2}=\sum_{n\ge 1}\frac{1}{n^2}=\zeta(2) \end{eqnarray}$
$I$ の２つ目の計算方法は変数変換です。
$\displaystyle u=\frac{y+x}{2},\ v=\frac{y-x}{2}$
と変数変換します。すると $x=u-v,y=u+v$ より
$\displaystyle\frac{1}{1-xy}=\frac{1}{1-u^2+v^2}$
である。またヤコビアンは $2$ である。
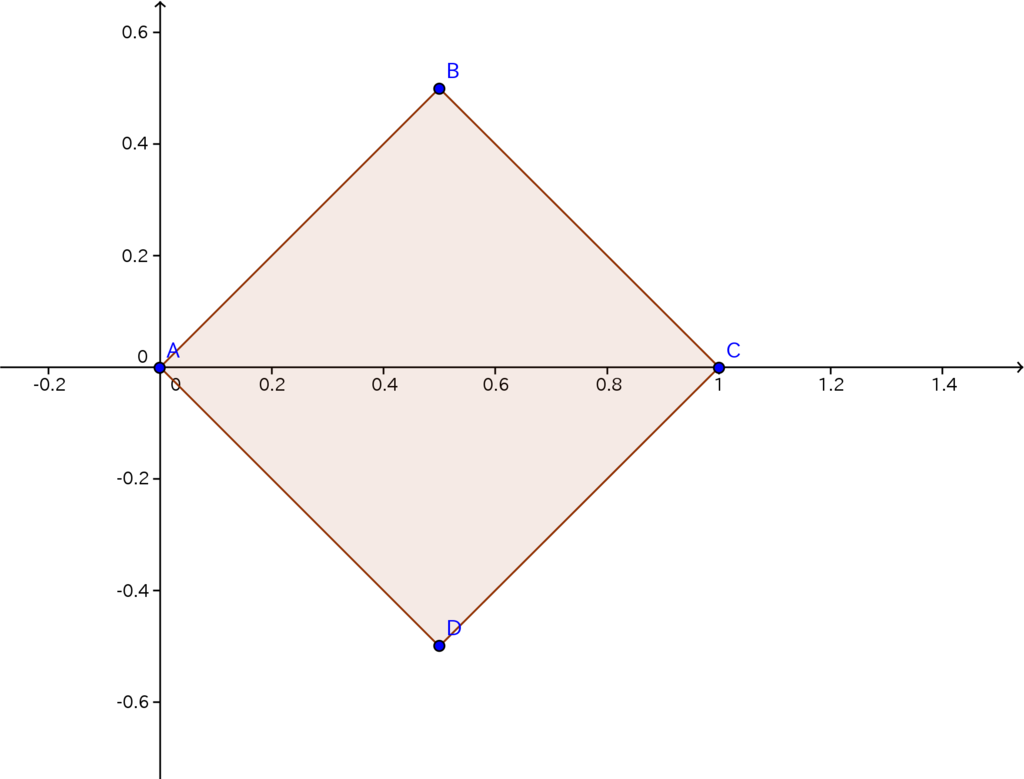
f:id:otaku_of_suri:20160703141457p:plain

f:id:otaku_of_suri:20160703141457p:plain

変数変換後の積分領域は上の図の色がけ部であるから $\displaystyle u\le \frac{1}{2}$ と $\displaystyle u\ge \frac{1}{2}$ に分けて積分する。また $v$ に関して対称であることも考慮すると
$\begin{eqnarray} I&=&4\int_0^{\frac{1}{2}}\left(\int_0^u\frac{dv}{1-u^2+v^2}\right)du+4\int_{\frac{1}{2}}^1\left(\int_0^{1-u}\frac{dv}{1-u^2+v^2}\right)du\\ &=&4\int_0^{\frac{1}{2}}\frac{1}{\sqrt{1-u^2}}\arctan\left(\frac{u}{\sqrt{1-u^2}}\right)du\\ &&+4\int_{\frac{1}{2}}^1\frac{1}{\sqrt{1-u^2}}\arctan\left(\frac{1-u}{\sqrt{1-u^2}}\right)du \end{eqnarray}$
となります。ここで $\displaystyle\int\frac{dx}{a^2+x^2}=\frac{1}{a}\arctan{\frac{x}{a}}+C$ を用いました。
ここで $u=\sin\theta$ とおくと、 $\displaystyle\frac{u}{\sqrt{1-u^2}}=\frac{\sin\theta}{\cos\theta}=\tan\theta$ であるから結局、 $\displaystyle\arctan{\frac{u}{\sqrt{1-u^2}}}=\arcsin u$ となります。
また $u=\cos\theta$ とおくと、 $\displaystyle\frac{1-u}{\sqrt{1-u^2}}=\frac{1-\cos\theta}{\sin\theta}=\frac{2\sin^2\frac{\theta}{2}}{2\cos\frac{\theta}{2}\sin\frac{\theta}{2}}=\tan\frac{\theta}{2}$ であるから結局、 $\displaystyle\arctan{\frac{1-u}{\sqrt{1-u^2}}}=\frac{1}{2}\arccos u$ となります。よって、
$\displaystyle I=4\int_0^{\frac{1}{2}}\frac{\arcsin u}{\sqrt{1-u^2}}du+2\int_{\frac{1}{2}}^1\frac{\arccos u}{\sqrt{1-u^2}}du$
がわかります。ここで第１項の積分については $u=\sin\theta$ 、第２項の積分については $u=\cos\theta$ と変数変換すると
$\begin{eqnarray} I&=&4\int_0^{\frac{\pi}{6}}\frac{\theta}{\cos\theta}\cos\theta d\theta+2\int_{\frac{\pi}{3}}^{0}\frac{\theta}{\sin\theta}(-\sin\theta)d\theta\\ &=&4\int_{0}^{\frac{\pi}{6}}\theta d\theta+2\int_{0}^{\frac{\pi}{3}}\theta d\theta\\ &=&4\left[\frac{\theta^2}{2}\right]^{\frac{\pi}{6}}_{0}+2\left[\frac{\theta^2}{2}\right]^{\frac{\pi}{3}}_{0}\\ &=&4\frac{1}{2}\frac{\pi^2}{36}+2\frac{1}{2}\frac{\pi^2}{9}=\frac{\pi^2}{6} \end{eqnarray}$
となります！！！以上より
$\displaystyle\zeta(2)=\frac{\pi^2}{6}$
が示されました。

あと１つ証明があるのでそれはまた今度ということで。