2016-07-25

弾性体の振動の縦波と横波

よねすけ物理

よねすけです。振動波動論の試験で弾性体の振動に関する問題が出て勉強してなくて全く分かりませんでした。つらい。。。

弾性体中の座標ベクトル $\textbf{r}$ の点の、時間 $t$ における変位を $\textbf{u}(\textbf{r},t)$ とすると、弾性体の振動の方程式は

$\displaystyle\rho\partial^2_{t}\textbf{u}=\frac{E}{2(1+\mu)}\left[\nabla^2\textbf{u}+\frac{1}{1-2\mu}\nabla(\nabla\cdot\textbf{u})\right]$
で与えられます。ここで $\rho$ は弾性体の密度、 $E$ はヤング率、 $\mu$ はポアソン比です。(いずれも定数、 $\displaystyle 0<\mu<\frac{1}{2}$ )

定ベクトル $\textbf{u}_0$ を用いて $\displaystyle\textbf{u}\left(\textbf{r},t)=\textbf{u}_0{\rm exp}(i(\textbf{k}\cdot\textbf{r}-\omega_k t)\right)$ と書けたとします。これを先の振動の式に代入して整理すると

$\displaystyle\rho\omega_k^2\textbf{u}_0=\frac{E}{2(1+\mu)}\left[k^2\textbf{u}_0+\frac{1}{1-2\mu}\textbf{k}(\textbf{k}\cdot\textbf{u}_0)\right]$
が得られます。
縦波の場合、すなわち考える波の進行方向と媒質の振動方向が平行な場合、
$\textbf{k}\parallel\textbf{u}_0$
が言えます。 $\textbf{k}(\textbf{k}\cdot\textbf{u}_0)=k^2\textbf{u}_0$ を代入すれば
$\displaystyle\rho\omega_k^2\textbf{u}_0=\frac{E}{2(1+\mu)}\left[k^2\textbf{u}_0+\frac{k^2}{1-2\mu}\textbf{u}_0\right]$
です。縦波の速さを $v_l$ とおくと $\omega_k=v_l k$ なので
$\displaystyle v_l=\sqrt{\frac{(1-\mu)E}{(1+mu)(1-2\mu)\rho}}$
が分かりました。

横波の場合、すなわち考える波の進行方向と媒質の振動方向が垂直な場合、

$\textbf{k}\cdot\textbf{u}_0=0$
が言えます。
$\displaystyle\rho\omega_k^2\textbf{u}_0=\frac{E}{2(1+\mu)}k^2\textbf{u}_0$
横波の速さを $v_t$ とおくと $\omega_k=v_t k$ なので
$\displaystyle v_l=\sqrt{\frac{E}{2(1+mu)\rho}}$
が分かりました。

縦波、横波の速さを比較してみましょう。

$\displaystyle\begin{eqnarray} \left(\frac{v_l}{v_t}\right)^2&=&\frac{(1-\mu)E}{(1+\mu)(1-2\mu)\rho}\frac{2(1+\mu)\rho}{E}\\ &=&1+\frac{1}{1-2\mu}\\ &>&2 \end{eqnarray}$
これより、 $v_l>\sqrt{2}v_t$ が分かります。
地震のP波 $(=v_l)$ の速さはおよそ $5\sim 7km/s$ 、地震のQ波 $(=v_t)$ の速さはおよそ $3\sim 4km/s$ と言われているそうなのでだいたい一致していますね。

それでは。

2016-07-16

無理数の無理数の無理数の・・・

よねすけ数学

こんにちは。世の大学生は試験前で忙しい頃ですね。僕ももれなく忙しいです。試験勉強頑張りましょうね。

少し前にtsujimotterさんのこの記事が話題になりました。
tsujimotter.hatenablog.com
この記事では $\displaystyle\sqrt{2}^{\sqrt{2}}$ を用いて無理数の無理数乗の中で有理数になるものが存在することの証明を行っていました。結果から言うと $\displaystyle\sqrt{2}^{\sqrt{2}}$ は超越数になります。(このことは
ゲルフォント＝シュナイダーの定理 - Wikipediaを用いるとすぐに分かります。)
では、次の値を考えてみましょう。

$\LARGE{\displaystyle\sqrt{2}^{\sqrt{2}^{\sqrt{2}^{\sqrt{2}^{\sqrt{2}^{\sqrt{2}^{\sqrt{2}^{\sqrt{2}^{\sqrt{2}^{\sqrt{2}^{\sqrt{2}^{\sqrt{2}^{\sqrt{2}^{\cdots}}}}}}}}}}}}}}$
なんじゃこれ、そもそも収束するのか？？って思わせる式ですね。
でもこれ、きちんと収束してくれるんですよ。しかも有理数に。不思議ですよね。 $\displaystyle\sqrt{2}^{\sqrt{2}}$ は超越数になるのに、その操作を無限回行うと有理数になる。無限というものの神秘を感じます。
以下に証明を示します。証明は理系の高校生ならわかるとてもシンプルなものになっています。

$\displaystyle\sqrt{2}^{\sqrt{2}^{\sqrt{2}^{\sqrt{2}^{\sqrt{2}^{\sqrt{2}^{\sqrt{2}^{\sqrt{2}^{\sqrt{2}^{\sqrt{2}^{\sqrt{2}^{\sqrt{2}^{\sqrt{2}^{\cdots}}}}}}}}}}}}}=2$
(証明)
与えられた式を次のように数列を用いて漸化式で書き換えます。
$\displaystyle a_n=\sqrt{2}^{a_{n-1}},a_0=\sqrt{2},s.t.\lim_{n\to\infty}a_n=2$
証明すべきことは $a_n$ が $2$ に収束することです。
まず $a_n<2$ を数学的帰納法により示します。 $n=0$ の時は明らかです。ある $n$ で $a_n<2$ だとすると
$a_{n+1}=\sqrt{2}^{a_n}<\sqrt{2}^2=2$
となり $n+1$ の場合も示されました。以上より $a_n<2$ です。
次に $f(x)=\sqrt{2}^x$ という関数を考えます。
$\displaystyle f'(x)=(\log{\sqrt{2}})\sqrt{2}^x$
となります。ここで平均値の定理を考えると区間 $(a_n,2)$ で
$\displaystyle\frac{f(2)-f(a_n)}{2-a_n}=f'(c_n)$
なる $c_n$ が存在します。 $c_n<2$ が分かっているので $f'(c_n) <\log 2$ です。これより
$\begin{eqnarray*} &&f(2)-f(a_n)=f'(c_n)(2-a_n)\\ &\Rightarrow&2-a_{n+1}<(\log 2)(2-a_n) \end{eqnarray*}$
が分かります。あとはこれを順番に用いると
$\begin{eqnarray*} 0<2-a_{n}&<&(\log 2)(2-a_{n-1})\\ &<&(\log 2)^2(2-a_{n-1})\\ &&\cdots\\ &<&(\log 2)^n(2-a_0) \end{eqnarray*}$
となります。 $\log 2<1$ より $n\to\infty$ の極限で
$2-a_n\to 0\Leftrightarrow a_n\to 2$
となりました。以上より $\displaystyle\lim_{n\to\infty}a_n=2$ が示されました。

高校生でも理解できる簡単な証明ですね。(これは多分同志社大学の数学の入試問題やった。)
一般に $a$ が自然対数の底 $e$ よりも小さな $1$ 以上の実数なら
$\begin{eqnarray*} \sqrt[a]{a}^{\sqrt[a]{a}^{\sqrt[a]{a}^{\sqrt[a]{a}^{\sqrt[a]{a}^{\sqrt[a]{a}^{\sqrt[a]{a}^{\sqrt[a]{a}^{\sqrt[a]{a}^{\sqrt[a]{a}^{\sqrt[a]{a}^{\cdots}}}}}}}}}}}=a \end{eqnarray*}$
が成立します。極限は奥が深いですね。
それでは。

2016-07-13

数学のメモその３

よねすけ数学フーリエ変換

今回は、一旦ゼータ関数を置いといてフーリエ解析に関することを書きます。
授業の中でPlancherel(プランシュレル)の定理というものを習いました、

Plancherelの定理
$f,g,\hat{g}\in L^1(\mathbb{R})\Rightarrow \langle\hat{f},\hat{g}\rangle=\langle f,g\rangle$
$f\in L^1(\mathbb{R})$ :有界連続 $\Rightarrow\|f\|=\|\hat{f}\|\ (f,\hat{f}\in L^2(\mathbb{R}))$

というものなんですが授業ではさらっと流されて証明もプリントで、、、みたいな感じやったんですけどこの定理は結構面白いことを言ってるんじゃないかなあと思いました。

適当な正規直交関数系 $\displaystyle \{f_i (x)\}_{i=1}^{\infty}$ を一つ考えてみましょう。正規直交関数系とは

$\begin{equation} \langle f_i,f_j\rangle=\delta_{i,j} \end{equation}$
を満たすもののことです。勘の良い方はこれで僕が何を言いたいのか分かったかも知れませんね笑。この関数が ${}^{\forall}i\in\mathbb{N}$ に関して $f_i(x)\in L^2(\mathbb{R})$ などなど適当な条件を満たしているとしましょう。 $f_i$ のFourier変換を $\mathcal{F}f_i=\hat{f}_i$ と書くことにすると、
$\langle \hat{f}_i,\hat{f}_j\rangle=\langle f_i,f_j\rangle=\delta_{i,j}$
がプランシュレルの定理から分かります。これが何を意味しているかというと適当な条件を満たす正規直交関数系をひとつ持ってこればそれをFourier変換して得られる系もまた正規直交関数系となるのです！！

教授氏にこのことについて質問してみると、チェビシェフの多項式においてこのことが成り立つそうです。また時間があるときに確かめてみたいです。
それでは。

2016-07-03

数学のメモその２

よねすけ数学バーゼル問題

前回に続き $\displaystyle\zeta(2)=\frac{\pi^2}{6}$ の証明を書きたいと思います。
〜２重積分を用いる〜
この証明は２重積分

$\begin{eqnarray} I=\int_0^1\int_0^1\frac{1}{1-xy}dxdy \end{eqnarray}$

の値を２通リに求めることからわかります。１つ目は $\displaystyle\frac{1}{1-xy}$ を等比級数 $\sum_{n\ge 0}(xy)^n$ に展開することです。
$\begin{eqnarray} I&=&\int_0^1\int_0^1(xy)^ndxdy=\sum_{n\ge 0}\int_0^1\int_0^1x^ny^ndxdy\\ &=&\sum_{n\ge 0}\left(\int_0^1x^ndx\right)\left(\int_0^1y^ndy\right)=\sum_{n\ge 0}\frac{1}{n+1}\frac{1}{n+1}\\ &=&\sum_{n\ge 0}\frac{1}{(n+1)^2}=\sum_{n\ge 1}\frac{1}{n^2}=\zeta(2) \end{eqnarray}$
$I$ の２つ目の計算方法は変数変換です。
$\displaystyle u=\frac{y+x}{2},\ v=\frac{y-x}{2}$
と変数変換します。すると $x=u-v,y=u+v$ より
$\displaystyle\frac{1}{1-xy}=\frac{1}{1-u^2+v^2}$
である。またヤコビアンは $2$ である。
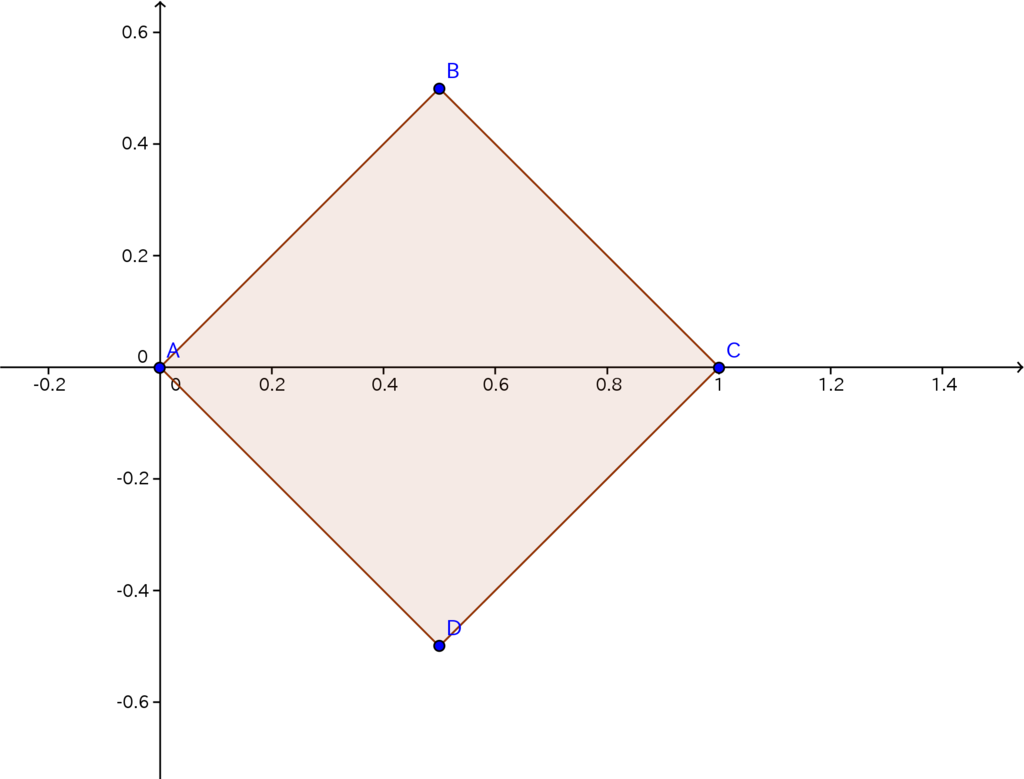
f:id:otaku_of_suri:20160703141457p:plain

f:id:otaku_of_suri:20160703141457p:plain

変数変換後の積分領域は上の図の色がけ部であるから $\displaystyle u\le \frac{1}{2}$ と $\displaystyle u\ge \frac{1}{2}$ に分けて積分する。また $v$ に関して対称であることも考慮すると
$\begin{eqnarray} I&=&4\int_0^{\frac{1}{2}}\left(\int_0^u\frac{dv}{1-u^2+v^2}\right)du+4\int_{\frac{1}{2}}^1\left(\int_0^{1-u}\frac{dv}{1-u^2+v^2}\right)du\\ &=&4\int_0^{\frac{1}{2}}\frac{1}{\sqrt{1-u^2}}\arctan\left(\frac{u}{\sqrt{1-u^2}}\right)du\\ &&+4\int_{\frac{1}{2}}^1\frac{1}{\sqrt{1-u^2}}\arctan\left(\frac{1-u}{\sqrt{1-u^2}}\right)du \end{eqnarray}$
となります。ここで $\displaystyle\int\frac{dx}{a^2+x^2}=\frac{1}{a}\arctan{\frac{x}{a}}+C$ を用いました。
ここで $u=\sin\theta$ とおくと、 $\displaystyle\frac{u}{\sqrt{1-u^2}}=\frac{\sin\theta}{\cos\theta}=\tan\theta$ であるから結局、 $\displaystyle\arctan{\frac{u}{\sqrt{1-u^2}}}=\arcsin u$ となります。
また $u=\cos\theta$ とおくと、 $\displaystyle\frac{1-u}{\sqrt{1-u^2}}=\frac{1-\cos\theta}{\sin\theta}=\frac{2\sin^2\frac{\theta}{2}}{2\cos\frac{\theta}{2}\sin\frac{\theta}{2}}=\tan\frac{\theta}{2}$ であるから結局、 $\displaystyle\arctan{\frac{1-u}{\sqrt{1-u^2}}}=\frac{1}{2}\arccos u$ となります。よって、
$\displaystyle I=4\int_0^{\frac{1}{2}}\frac{\arcsin u}{\sqrt{1-u^2}}du+2\int_{\frac{1}{2}}^1\frac{\arccos u}{\sqrt{1-u^2}}du$
がわかります。ここで第１項の積分については $u=\sin\theta$ 、第２項の積分については $u=\cos\theta$ と変数変換すると
$\begin{eqnarray} I&=&4\int_0^{\frac{\pi}{6}}\frac{\theta}{\cos\theta}\cos\theta d\theta+2\int_{\frac{\pi}{3}}^{0}\frac{\theta}{\sin\theta}(-\sin\theta)d\theta\\ &=&4\int_{0}^{\frac{\pi}{6}}\theta d\theta+2\int_{0}^{\frac{\pi}{3}}\theta d\theta\\ &=&4\left[\frac{\theta^2}{2}\right]^{\frac{\pi}{6}}_{0}+2\left[\frac{\theta^2}{2}\right]^{\frac{\pi}{3}}_{0}\\ &=&4\frac{1}{2}\frac{\pi^2}{36}+2\frac{1}{2}\frac{\pi^2}{9}=\frac{\pi^2}{6} \end{eqnarray}$
となります！！！以上より
$\displaystyle\zeta(2)=\frac{\pi^2}{6}$
が示されました。

あと１つ証明があるのでそれはまた今度ということで。

2016-06-17

数学のメモ

よねすけ数学バーゼル問題

授業の演習問題で $\displaystyle\zeta(2)=\frac{\pi^2}{6}$ の証明する問題が出たのでいろいろな証明を載せたいと思います。

～フーリエ級数展開の利用～
$\displaystyle\zeta(2)=\sum_{n=0}^{\infty}\frac{1}{n^2}$ についてこれは無限級数なのでフーリエ級数展開を用いることを考えます。(授業の演習問題はこの方法だった)
周期関数 $f(t)=t^2(-\pi\le t\le\pi)$ の複素フーリエ級数展開を計算すると

$\displaystyle \begin{equation} t^2=\frac{\pi^2}{3}+\sum_{n\ne 0,n=-\infty}^{\infty}\frac{2(-1)^n}{n^2}e^{-int} \end{equation}$
である。 $t=\pi$ を代入すると
$\displaystyle\begin{eqnarray} \pi^2&=&\frac{\pi^2}{3}+\sum_{n\ne0}\frac{2(-1)^n}{n^2}e^{-int}\\ &=&\frac{\pi^2}{3}+\sum_{n\ne0}\frac{2(-1)^n}{n^2}(-1)^n\\ &=&\frac{\pi^2}{3}+\sum_{n\ne0}\frac{2}{n^2}\\ &=&\frac{\pi^2}{3}+2\sum_{n=1}^{\infty}\frac{2}{n^2}\\ &=&\frac{\pi^2}{3}+4\sum_{n=1}^{\infty}\frac{1}{n^2} \end{eqnarray}$

となります。あとは式変形すると
$\displaystyle \sum_{n=1}^{\infty}\frac{1}{n^2}=\frac{\pi^2}{6}$

となることがわかりました。

～別の級数から求める～
先ほどの関数の複素でない場合のフーリエ級数展開から得られる

$\displaystyle \sum_{n=1}^{\infty}\frac{(-1)^{n+1}}{n^2}=\frac{\pi^2}{12}$
があります。これを書き下してみると
$\displaystyle \frac{1}{1^2}-\frac{1}{2^2}+\frac{1}{3^2}-\frac{1}{4^2}+\frac{1}{5^2}-\frac{1}{6^2}+\cdots=\frac{\pi^2}{12}$
一方、適切な不等式評価を行うと $\displaystyle\sum_{n=1}^{\infty}\frac{1}{n^2}$ は収束することがわかるので、この値を $\displaystyle\alpha$ と置いてみます。
ここで以下のような級数を考えます。
$\displaystyle 2\frac{1}{2^2}+2\frac{1}{4^2}+2\frac{1}{6^2}+2\frac{1}{8^2}+\cdots$
この級数はきちんと収束して先ほどの $\displaystyle\alpha$ を用いると $\displaystyle 2\cdot\frac{1}{2^2}\alpha=\frac{1}{2}\alpha$ となります。
そこでこの2つの無限級数を足し合わせてみます。
$\displaystyle\begin{eqnarray} \frac{1}{1^2}-\frac{1}{2^2}+\frac{1}{3^2}-\frac{1}{4^2}+\frac{1}{5^2}-\frac{1}{6^2}+\cdots&=&\frac{\pi^2}{12}\\ 2\frac{1}{2^2}+2\frac{1}{4^2}+2\frac{1}{6^2}+2\frac{1}{8^2}+\cdots&=&\frac{1}{2}\alpha \end{eqnarray}$
すると左辺はちょうど $\displaystyle\frac{1}{1^2}+\frac{1}{2^2}+\frac{1}{3^2}+\cdots=\sum_{n=1}^{\infty}\frac{1}{n^2}$ となり、これは $\displaystyle\alpha$ に一致します。右辺と比較すると $\displaystyle\frac{\pi^2}{12}+\frac{1}{2}\alpha=\alpha$ より、
$\displaystyle \alpha=\frac{\pi^2}{6}$
が得られました。

続きは長くなるので次回に書きます。

2016-06-01

C++で8パズルをA探索、IDA探索を用いて解いた

zalgo PC

授業で8パズルの探索を図示する課題があったんだけど、どうせならってことでプログラムを書いた。

A*アルゴリズムと言うのは、推定関数h(x)を使って、ゴールまでの距離を推定して、今までの探索の深さとの合計によってそのノードの評価値f(x)を決めて、それを元に最良優先探索をするアルゴリズムのこと。
IDA*アルゴリズムは、A*と同じようにf(x)を決めて、cutoff以下のf(x)の点だけを展開して深さ優先探索して、詰んだらcutoffを増やしてやり直し、っていうアルゴリズム（反復深化+A*みたいなかんじ）

コマンドライン引数で、
1:A*,推定関数は位置が違うパズルの数
2:A*,推定関数はマンハッタン距離
3:IDA*,推定関数は位置が違うパズルの数
4:IDA*,推定関数はマンハッタン距離

出力の方法が雑魚いのは勘弁して下さい＼(^o^)／

#include <iostream>
#include <cstdlib>
#include <functional>
#include <queue>
#include <stack>
#include <map>
#include <vector>

struct state {
    int puzzle[9];
    int depth;
    int evaluation;
    bool operator>(const state &s) const {
        return evaluation > s.evaluation;
    }
};

state start = { {1, 2, 3,
                4, 5, 6,
                7, 8, 0},
                0,
                0};
state goal = { {4, 1, 5,
                 0, 3, 2,
                 7, 8, 6}, // puzzle
                0,           // depth
                0};        // evaluation
std::priority_queue <state, std::vector<state>, std::greater<state> > open;
std::stack<state> open2;
std::vector<state> closed;
int count = 0;
int max = 0;

bool IsFinished(state s)
{
    for (int i = 0; i < 8; i++) {
       if (s.puzzle[i] != goal.puzzle[i]) {
           return false;
       } 
    }
    return true;
}

int ManhattanOne(int n, int place)
{
    if (goal.puzzle[n] == 0) {
        return 0;
    }
    int q, r;
    q = abs(place / 3 - n / 3);
    r = abs(place % 3 - n % 3);
    return q + r;
}

int manhattan(state s)
{
    int eval = 0;
    std::map<int, int> goalplace;
    for (int i = 0; i < 9; i++) {
        goalplace[goal.puzzle[i]] = i;
    }
    for (int i = 0; i < 9; i++) {
        eval += ManhattanOne(goalplace[s.puzzle[i]], i);
    }
    return eval;
}

int wrong(state s)
{
    int eval = 0;
    for (int i = 0; i < 9; i++) {
        if (s.puzzle[i] != 0 and s.puzzle[i] != goal.puzzle[i]) {
            eval++;
        }
    }
    return eval;
}

void PrintState(state s)
{
    std::cout << '|' << s.puzzle[0] << '|' << s.puzzle[1] << '|' << s.puzzle[2] << '|' << ' ' << count << std::endl;
    std::cout << '|' << s.puzzle[3] << '|' << s.puzzle[4] << '|' << s.puzzle[5] << '|' << " f(n) = " << s.evaluation << std::endl;
    std::cout << '|' << s.puzzle[6] << '|' << s.puzzle[7] << '|' << s.puzzle[8] << '|' << " g(n) = " << s.depth << std::endl << std::endl;
    return;
}

bool IsSamePuzzle(state s1, state s2)
{
    for (int i = 0; i < 9; i++) {
        if (s1.puzzle[i] != s2.puzzle[i]) {
            return false;
        }
    }
    return true;
}

bool InClosed(state s)
{
    for (int i = 0; i < closed.size(); i++) {
        if (IsSamePuzzle(s, closed[i])) {
            return true;
        }
    }
    return false;
}

void AStar(std::function<int(state)> fun)
{
    if (open.empty()) {
        std::cerr << "Search have mistakenly stopped!" << std::endl;
    }
    if (max < open.size() + closed.size()) {
        max = open.size() + closed.size();
    }
    count++;
    state now = open.top();
    open.pop();
    closed.push_back(now);
    PrintState(now);
    if (IsFinished(now)) {
        std::cout << "Finished!" << std::endl;
        return;
    }
    state s = now;    
    int zero;
    for (int i = 0; i < 9; i++) {
        if (now.puzzle[i] == 0) {
            zero = i;
            break;
        }
    }
    if (zero - 3 >= 0) {
        std::swap(s.puzzle[zero - 3], s.puzzle[zero]);
        if (not InClosed(s)) {
            s.depth++;
            s.evaluation = fun(s) + s.depth;
            open.push(s);
        }
        s = now;
    }
    if (zero % 3 != 0) {
        std::swap(s.puzzle[zero - 1], s.puzzle[zero]);
        if (not InClosed(s)) {
            s.depth++;
            s.evaluation = fun(s) + s.depth;
            open.push(s);
        }
        s = now;
    }
    if (zero % 3 != 2) {
        std::swap(s.puzzle[zero + 1], s.puzzle[zero]);
        if (not InClosed(s)) {
            s.depth++;
            s.evaluation = fun(s) + s.depth;
            open.push(s);
        }
        s = now;
    }
    if (zero + 3 < 9) {
        std::swap(s.puzzle[zero + 3], s.puzzle[zero]);
        if (not InClosed(s)) {
            s.depth++;
            s.evaluation = fun(s) + s.depth;
            open.push(s);
        }
    }
    AStar(fun);
    return;
}

void IDAStar_rep(std::function<int(state)> fun, int c)
{
    if (open2.empty()) {
        std::cout << c << " roop end" << std::endl;
        c++;
        open2.push(start);
        closed.clear();
        IDAStar_rep(fun, c);
        return;
    }
    if (max < open2.size() + closed.size()) {
        max = open2.size() + closed.size();
    }
    state now = open2.top();
    closed.push_back(now);
    open2.pop();
    count++;
    if (IsFinished(now)) {
        PrintState(now);
        std::cout << "Finished!" << std::endl;
        return; 
    }
    state s = now;
    PrintState(now);
    int zero;
    for (int i = 0; i < 9; i++) {
        if (now.puzzle[i] == 0) {
            zero = i;
            break;
        }
    }
    if (zero - 3 >= 0) {
        std::swap(s.puzzle[zero - 3], s.puzzle[zero]);
        if (not InClosed(s)) {
            s.depth++;
            s.evaluation = fun(s) + s.depth;
            if (s.evaluation <= c) {
                open2.push(s);
            }
        }
        s = now;
    }
    if (zero % 3 != 0) {
        std::swap(s.puzzle[zero - 1], s.puzzle[zero]);
        if (not InClosed(s)) {
            s.depth++;
            s.evaluation = fun(s) + s.depth;
            if (s.evaluation <= c) {
                open2.push(s);
            }
        }
        s = now;
    }
    if (zero % 3 != 2) {
        std::swap(s.puzzle[zero + 1], s.puzzle[zero]);
        if (not InClosed(s)) {
            s.depth++;
            s.evaluation = fun(s) + s.depth;
            if (s.evaluation <= c) {
                open2.push(s);
            }
        }
        s = now;
    }
    if (zero + 3 < 9) {
        std::swap(s.puzzle[zero + 3], s.puzzle[zero]);
        if (not InClosed(s)) {
            s.depth++;
            s.evaluation = fun(s) + s.depth;
            if (s.evaluation <= c) {
                open2.push(s);
            }
        }
        s = now;
    }
    IDAStar_rep(fun, c);
    return;
}

void IDAStar(std::function<int(state)> fun)
{
    IDAStar_rep(fun, open2.top().evaluation);
    return;
}

int main(int argc, char *argv[])
{
    if(argc != 2) {
        std::cerr << "Usage: <Executable filename> <type number>" << std::endl; 
        exit(0);
    }

    std::function< int(state) > fun;
    std::function< void(std::function< int(state) >) > alg;

    switch (*argv[1]) {
        case '1':
                 fun = wrong;
                 alg = AStar;
                 break;
        case '2':
                 fun = manhattan;
                 alg = AStar;
                 break;
        case '3':
                 fun = wrong;
                 alg = IDAStar;
                 break;
        case '4':
                 fun = manhattan;
                 alg = IDAStar;
                 break;
    }
    start.evaluation = fun(start);
    open.push(start);
    open2.push(start);
    alg(fun);

    std::cout << "Most saved nodes: " << max << std::endl;

    return 0;
}

結果は、以下のとおり
1のとき、28手、メモリに保存したノードの数52
2のとき、21手、メモリに保存したノードの数35
3のとき、33手、メモリに保存したノードの数17
4のとき、10手、メモリに保存したノードの数12

IDA*つえー

2016-05-28

行列の固有値計算のJacobi法をpythonで実装した

zalgo PC 数学

数値計算ライブラリのnumpyはほんとに便利。

import numpy as np

def jacobi(A,N,check):
    B = np.fabs(A - np.diag(list(np.diag(A))))
    nondiagmax = np.max(B)
    while nondiagmax > check:
        k = int(np.argmax(B) / 3)
        m = np.argmax(B) % 3
        cos2phi = np.fabs(A[k,k] - A[m,m]) / \
                np.sqrt(4.0 * A[k,m]**2 + (A[k,k] - A[m,m])**2)
        cosphi = np.sqrt((1.0 + cos2phi) / 2.0)
        sinphi = np.sign(-A[k,m] * (A[k,k] - A[m,m])) * \
                np.sqrt((1.0 - cos2phi) / 2.0)
        P = np.matrix(np.identity(N))
        P[k,k] = cosphi
        P[k,m] = sinphi
        P[m,k] = -sinphi
        P[m,m] = cosphi
        A = ((P.T).dot(A)).dot(P)
        B = np.fabs(A - np.diag(list(np.diag(A))))
        nondiagmax = np.max(B)
    print(A)
    print(np.diag(A))

if __name__ == "__main__":
    EPS = 1e-8
    N = 3
    A = np.matrix([[3.0,0.01,0.1],[0.01,2.0,0.1],[0.1,0.1,1.0]])
    print(A)
    jacobi(A,N,EPS)

結果より、固有値は、[ 3.00521156 2.00950971 0.98527872]

オタクof数理の共同ブログ

京大情報学科数理工学コースの学生4人による共同ブログです